
|
Filosofibiblioteket Om meg Bokmerker i dette dokumentet |
LOGIKK
Denne artikkelen ble skrevet rundt 1990. Her er en del «kjedelig» logikk som andre sikkert kunne skrevet mye bedre enn meg. Her er det noen vesentlige konklusjoner som er viktig å ta med seg:
Det at et tankesystem er logisk uten selvmotsigelser betyr ikke at det har noe med virkeligheten å gjøre.
1. Deduksjon er en sikker konklusjon dersom den er gjort korrekt og premissene er sikre.
2. Induksjon er derimot en usikker konklusjon.
3. Jeg kaller gjerne en avgrenset virkelighetsbeskrivelse som er uten logiske selvmotsigelser for en lukket forklaringsmodell. Det kalles også for en referansemodell. Det er viktig å være klar over at selv om modellen stemmer presist med virkeligheten så beviser ikke det at modellen har noe med virkeligheten å gjøre. Det er fullt mulig at det samme sett av fenomener kan beskrives like godt ved hjelp av en annen modell.
4. Tankemodeller som inneholder enkle altomfattende forklaringer på alt kaller jeg for lukkede eksistensialmodeller. Har vi samme resonnement som for lukkede forklaringsmodeller. Det lukkede postulat kan ikke bevises bare fordi modellen forklarer alt. Det finnes mange modeller som forklarer alt.
Det er morsomt i dag å se at jeg eksperimenterte med en slags symbolforening mellom mengdelæren og Booles algebra. Hva jeg skulle med det, aner jeg ikke.
Det mest essensielle avsnittet er det om teksttolkning. Disse tankene om det
naturlige språks elastisitet har formet mye av min tenkning videre. Det har
dannet basis for refleksjoner om hvordan vi kan fanges av språk og logikk i vår
måte å forstå virkeligheten
på. Vi tenderer til å forveksle det mentale kartet med virkeligheten, tillegge begrepene
selvstendig eksistens, og gjøre vår logiske
sans til en allmenngyldig lov i naturen.
Det fikk meg også til å få opp øynene for begreper. Begrepenes innhold er ikke
absolutt. Enhver står fritt til å bruke begrepene på sin måte, men kravet er at
det da må defineres. Jeg har også blitt klar over at udefinert bruk av begreper
kan gi sterke retoriske
eller propagandistiske effekter.
Refleksjonene rundt lukkede
eksistensialmodeller er også aktuell lesning. Jeg har senere utviklet
refleksjonen om virkelighetsoppfatning.
Lukkede eksistensialmodeller hører inn som en gjennomgripende del av
virkelighetsoppfatningen.
Mitt metafysiske syn på logikken har jeg beskrevet her.
Tradisjonell logikk er læren om tankenødvendige
slutninger fra premiss til konklusjon (resonnementer). I vårt århundre har
imidlertid deler av logikken sprengt disse grenser og omfatter nå alle typer
slutninger, og metodelære. I vårt århundre har også logikken skilt seg ut som
egen vitenskap. Sentralt i denne prosessen stod den engelske filosofen Bertrand
Russell. I 1910 avsluttet han, i samarbeid med filosofen og matematikeren A.N.Whitehead
et kjempeverk, Principia Mathematica. Her ble grunnlaget lagt for den såkalte
symbolske logikken. Her er all bevisføring gjort ved hjelp av abstrakte
symboler. Ord, som vi finner i en vanlig matematikkbok, - og, eller,
anta at osv. - er erstattet med symboler. Dette verket viser klart
sammenhengen mellom matematikk og logikk. All matematikk kan føres tilbake til
enkle logiske setninger. Noen av dem virker nokså banale: «Hvis p er sann så er
p sann», «hvis p er sann eller p er sann så er p sann». Russell fremhever at de
deler av matematikken som virker mest umiddelbart innlysende, på sett og vis utgjør
de midterste etasjer i matematikkens bygning. Slikt som at to og to er fire.
Høyere opp, altså avledet ved lengre beviskjeder, finner vi mindre umiddelbart
innlysende ting, f.eks. at ![]() . I kjelleretasjene
finner vi setninger som er helt eiendommelige. Likevel faller bygningen dersom
kjelleretasjen er usolid.
. I kjelleretasjene
finner vi setninger som er helt eiendommelige. Likevel faller bygningen dersom
kjelleretasjen er usolid.
Så spørs det hvor solid den kjelleretasjen egentlig er. Russell jaktet utrettelig på selvmotsigelser. Der han fant dem, brukte han kniven; bort med dem. Men er ikke dette en forutsetning i seg selv? Er den absolutte virkelighet uten selvmotsigelser? Går det an at dersom p er sann, så er p ikke sann? Går det an å krangle på en så banal setning som det? Ja faktisk gjør det det. Setningen forutsetter nemlig at det finnes bare en sannhet. Det finnes bare en virkelighet. Men hvordan vet vi det? La oss tenke oss at det fantes to virkeligheter, og den en er komplementær til den andre. Da er det som er sant i den ene virkeligheten, ikke sant i den andre. En overgang fra den ene virkeligheten til den andre måtte da bli at dersom p er sann så er p ikke sann. I den andre virkeligheten ville f.eks. 2 + 2 = alle tall men ikke 4. Vi kan altså ikke bevise at vår menneskelige logikk er den eneste mulige. Vi er altså nødt til å ta en del forutsetninger for i det hele tatt å komme videre. Hvor sikker er så en slutning som er nødvendig ut fra våre logiske lover? Noen mener den er 100 %, jeg tenker at det vet jeg ikke, jeg regner slutningen for å være like sikker som logikken. En av de logiske setninger Russell kom frem til var:
Et hvert utsagn om en mengde A av utsagn som sier noe om alle utsagn i A er logisk meningsløst.
Dersom jeg skriver: «Alle utsagn i denne bok er feil», skulle dette rammes av Russells setning. I dette tilfellet er det lett og se, fordi utsagnet kan føre til en logisk ubestemt tilstand. Dersom alle utsagn i denne boken var feil, ville jo utsagnet være riktig, men da var det jo et utsagn i boken som var riktig, ergo må det være feil.
Hvor langt vi kan strekke en slik setning er vel uklart, men det er jo nærliggende å spørre om ikke noe slikt også gjelder for logiske konklusjoner. Kan jeg bruke min logikk til å produsere den konklusjonen at alt min logikk produserer er 100 % sikker? Her er parallellen med Russells setning slående, for det hele minner mistenkelig om sirkelbevis:
- Det min logikk sier er 100 % sikkert.
- Hvordan vet jeg det?
- Fordi min logikk har sagt det
- Hvordan vet jeg at min logikk snakker sant?
- Fordi det min logikk sier er 100 % sikker
Nå er de fleste av oss atskillig mindre nøyaktige, og vi har atskillig mindre kapasitet enn f.eks. Russell. Av denne grunn har jeg lært meg ikke å stole mer på min egen fornuft mer enn jeg må. Selv slike kapasiteter som Einstein kunne ta feil iblant, hvordan blir det ikke da med meg? Mine slutninger regner jeg derfor for å være like sikre som min fornuft, og den er slett ikke sikker. Denne erkjennelsen har virket frigjørende på meg. Den gjør meg mer åpen, både for mine egne og andres ideer.
Jeg har ikke tenkt på noen generell gjennomgang av logikken fordi det ville føre langt ut over denne bokas rammer, men jeg tar opp en del spesialemner fra logikken. Disse vil jeg anvende senere i boka.
Det er sagt at dersom Leibniz logiske skrifter var blitt kjent på hans tid, ville utviklingen av den moderne matematiske logikk kommet mye tidligere. Leibniz hevdet at logikken måtte oppfattes som en universell matematikk. Det var studiet av Aristoteles slutningslære som brakte ham på disse tanker. Leibniz formulerte slutningslæren ved hjelp av matematiske symboler. Hensikten med det var at man ved hjelp av et enkelt sett regneregler kunne regne seg frem til om en slutning var logisk gyldig eller ikke. Leibniz store drøm var å kunne beskrive all kunnskap ved hjelp av et spesifisert sett av grunnbegreper. Vitenskapelige uenigheter skulle man kunne regne seg bort fra. I stedet for vanlig argumentasjon tok man frem kalkulatoren, for å si det moderne.
Midt på 1800 tallet grunnla den engelske matematikeren og logikeren George Boole den moderne formallogikken. Denne skulle vise seg å få større betydning enn han ante. Hele datamaskinteknikken og mye av elektronikken bygger på Booles postulater.
Her er Booles postulater:
|
P1 |
0+0=0 |
|
P2 |
0+1=1+0=1 |
|
P3 |
1+1=1 |
|
P4 |
(-1)=0 |
|
P5 |
0*0=0 |
|
P6 |
0*1=1*0=0 |
|
P7 |
1*1 =1 |
|
P8 |
(-0)=1 |
|
|
|
Til å begynne med kan nok dette se litt forvirrende ut. Men la oss nå se litt på operatorene:
+ betyr eller
* betyr og
(-) betyr ikke
Verdiene er sannhetsverdier, dvs. de kan kun være sann (1) eller ikke-sann (0)
Vi innfører nå variabler instedet for sannhetsverdier:
|
P1 |
X+X=X |
|
P2 |
(-X)+X=1 |
|
P3 |
X+1=1 |
|
P4 |
X+0=X |
|
P5 |
X*X=X |
|
P6 |
(-X)*X=0 |
|
P7 |
X*1=1 |
|
P8 |
X*0=0 |
Utrykket (p = 50) er sant (1) dersom p = 50 . I alle andre tilfeller er utrykket ikke sant (0).
P1 kan skrives:
A er sann dersom (P = 50) eller (P = 50)
Når er A sann? Jo det vil avhenge fullstendig av om P = 50.
P2:
A er sant dersom (P <> 50) eller (P = 50)
Vi ser at A må bli sann uavhengig av verdien til P
P3:
A er sant dersom (P = 50) eller sant.
Vi får samme resultat som P2
P4:
A er sann dersom P = 50 eller ikke sant
Sannhetsverdien vil avhenge av verdien på P
(Prøv selv tilsvarende resonnementer for OG-operatoren)
Dersom disse postulatene stemmer hvilken praktisk betydning, får det? Jo de forteller noe vi egentlig alle vet fra før av:
X = (Døra er åpen )
Y = ( Det er kalt ute)
F = (Det er kaldt inne)
Mellom variablene X, Y og F eksisterer det følgende logiske sammenheng: F = X * Y
Dersom (det er kalt ute) og (døra er åpen) er (det er kalt inne) sant.
Ut fra dette kan vi sette opp en sannhetstabell for F:
|
N XYF |
|
|
1 000 |
(-X)*(-Y)=(-F) |
|
2 010 |
(-X)*Y=(-F) |
|
3 100 |
X*(-Y)=(-F) |
|
4 111 |
X*Y=F |
Vi prøver med alle kombinasjoner av X og Y og finner betingelsene for at X er sann.
1 sier:
Dersom ikke (døra er åpen) og ikke (det er kalt ute) så er det ikke (kaldt
inne)
2 sier:
Dersom Ikke (døra er åpen) og (det er kalt ute) så er det ikke (kaldt inne)
4 sier:
Dersom (døra er åpen) og (det er kalt ute) så er det (kaldt inne)
Vi omdefinerer nå Y:
Y = (Vinduet er åpent)
F = X + Y
Det eksisterer nå følgende sammenheng mellom variablene X,Y og F:
Dersom (døra er åpen) eller (vinduet er
åpent) er det (kaldt inne)
Ved å prøve alle mulige kombinasjoner av X og Y kommer vi frem til følgende
sannhetstabell:
|
N XYF |
|
|
1 000 |
(-X)+(-Y)=(-F) |
|
2 010 |
(-X)+Y=F |
|
3 100 |
X+(-Y)=F |
|
4 111 |
X+Y=F |
Prøv selv med tilsvarende resonnement. Dette er enkel logikk. Alle bruker vi dem til daglig når vi resonerer, de fleste av oss tenker ikke over det (kunnskapen er intuitiv)
Ved å formalisere disse enkle logiske regler og finne de postulater de bygger på, kan vi begynne å regne på logikken. Det vil føre forlangt å gå inn på regning med Booles algebra i denne sammenheng, men jeg vil likevel nevne at her finnes det algebraiske egenskaper som ligner en del på de vi finner i vanlig matematikk. I tillegg til den tradisjonelle Booles algebra finnes det også standardiserte metoder for å forenkle kompliserte logiske utrykk til enklere.
F.eks. kan ha uttrykket:
F = (-(A * B))(C + (-B))
reduseres til:
F = (-A) * C + (-B)
Innenfor digitalteknikken, som er grunnlaget for datamaskinteknikken, er denne type matematikk alfa omega.
Mengder er et kjent begrep fra matematikken. De objektene som inngår i en mengde kalles elementer. Her er f. eks tallene splittet opp i mengder, alt etter deres egenskaper:
1 N = De naturlige tall (Alle positive heltall; 1,2,3,4,5 osv.)
2 N0 = De naturlige heltall inkludert 0.
3 Z = Alle heltall (..-2,-1,0,1,2,2..)
4 Q = Alle tall som kan skrives som brøk
5 R = Alle reelle tall (Inkluderer også tall som PI, roten av 2)
R inkluderer altså alle tall som finnes på tallinjen. Men den utelukker de imaginære tallene som befinner seg utenfor tallinjen.
Vi ser fort at alle N må inngå i R. Vi sier at N er en delmengde av R. Ved hjelp av såkalte venn-diagrammer kan vi beskrive de forskjellige mengdene i forhold til hverandre. Tallenes oppdeling kan beskrives som på fig. 7.3.2
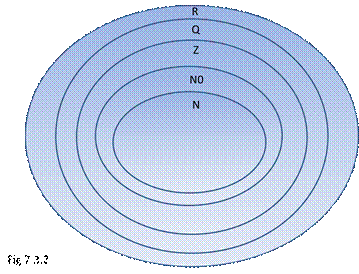
At element a inngår i mengden X kan skrives slik:
a ∈ X (a er et element i X)
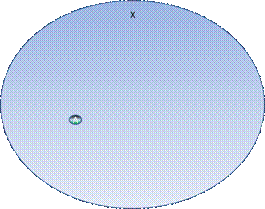
Fig 7.3.3 a er et element i x
Et element kan godt inngå i flere mengder. Dersom vi ønsker alle de elementene som er i A eller i B, eller i begge skrives dette slik:
A ∪ B (A union B)

Fig 7.3.4 A union B (skravert felt er den mengden som plukkes ut)
Dersom vi ønsker alle elementene som inngår i A og som samtidig inngår i B, skrives dette slik:
A ∩ B (A snitt B)
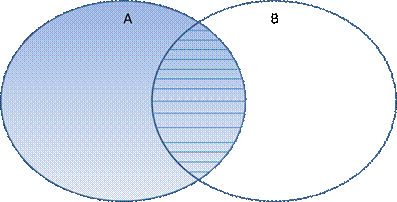
Fig 7.3.5 A snitt B
Dersom vi ønsker alle elementer som inngår i A men som ikke inngår i B skrives dette slik:
A \ B (A differens B)
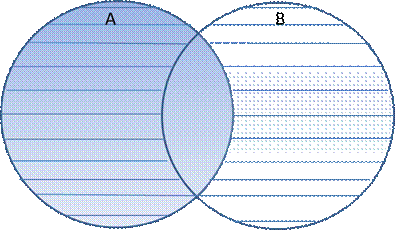
Fig 7.3.6 A differens D
Litt om mengde-utsagn:
Bl.a. disse ordene brukes dagligdags for å beskrive mengder:
- -ingenting
- -litt
- -noen
- -mange
- -alle
- -alt
Slik som de brukes i språket vårt er det ingen av dem som ikke kan virke tvetydig eller vagt. Spesielt kan ordene "ingenting" og "alle/ alt" være opphav til misforståelser dersom setningene blir tatt ut av sin sammenheng.
Fullstendig uavgrenset omfatter "alt" alt. Og alt, det må være alt som eksisterer eller kan tenkes å eksistere. I så måte er ordet "alt" det kraftigste vi har. Men svært ofte betyr ikke "alt" alle objekter i hele universet. Utsagnet "han spiste opp alt" betyr ikke at han spiste hele universet, men at han spiste opp all den maten som det var snakk om. Det er altså en underliggende forutsetning, som vi alle automatisk gjør, som avgrenser mengden. Lignende betraktninger kan gjøres på "ingen / ingenting". Dersom det er tvil må vi derfor analysere slike utsagn for å se hvilken mengde det kan være snakk om.
Ord som "litt», "få», "mange" er vage. Den utrykker delmengder som antyder noe om forholdet til den totale mengde. "få" antyder en delmengdemengde på under 50 % av totalmengden, helst mye under, men "mange" ligger over 50 %.
Når vi snakker om elementer i en mengde tenker vi oss at alle har identiske egenskaper. Et element kan ikke skilles fra et annet på noen annen måte enn den mengde det inngår i. Når vi skulle plukke ut elementer fra noen mengder brukte vi kriteriene tilhører / tilhører ikke den og den mengden for å avgjøre om elementet skulle plukkes ut. I praksis har vi som regel behov for helt andre kriterier for å kunne selektere (utvelge) elementer. Men da må vi bort fra begrepet "element" fordi det antyder noe konformt, dvs. uten bestemte individuelle egenskaper eller. Vi innfører begrepet "entitet" i stedet, for å angi at det dreier seg om objekter som har individuelle egenskaper. De individuelle egenskapene kalles for attributter. "Entitet" betyr egentlig væren, eller vesen. Det er altså et objekt som vi kan tenke på. Det behøver ikke å være noe fysisk objekt. Et ekteskap kan godt kalles for en entitet. Den mannen og den damen som utgjør ekteskapet kan, i andre sammenhenger, sees på som selvstendige entiteter. En entitet er altså en abstraksjon, og behøver nødvendigvis ikke å ha noen fysisk ekstensjon.
Entiteter er elementer i entitetsklasser. Når vi skal definere en entitetsklasse må vi velge klassens avgjørende attributter; vi må spesifisere de attributtene en entitet må ha for å kunne inngå i den bestemte entitetsklassen. Dette kan kalles for en deklarasjon av entitetsklassen. Ved en deklarasjon bestemmer vi de regler som skal anvendes for klassifikasjon av entiteter. For fysiske objekter er ikke dette annet enn realdefinisjoner. For epler kan det f.eks. være: "frukt som vokser på epletrær." For abstraksjoner eller begreper er dette nominaldefinisjoner. F.eks. hva er et ekteskap[1]? Det utgjøres av en mann og en kvinne, som har inngått en pakt med hverandre. Ekteskapet har en vigselsdato, det har en vigselsattest, det er registrert i folkeregisteret osv. Hvor klart og tydelig en slik definisjon, må være, avhenger av bruken. Et objekt kan godt være flere entiteter, fordi entiteten er en abstrakt konstruksjon. En mann kan f.eks. tilhøre entitetsklassen "bussjåfør" og "ektemann".
Når entitetsklassen er deklarert har vi muligheten til å identifisere de objekter som er entiteter i entitetsklassen. Dette kalles for klassifikasjon. Klassifikasjon kan skje positivt eller negativt. Ved positiv klassifikasjon må alle de avgjørende attributtene til testobjektet identifiseres. Dersom alle er identifisert, har vi en positiv klassifikasjon. Objektet er da identifisert som en entitet i entitetsklassen. Hvert eneste objekt som havner i entitetsklassen må ha positiv bekreftelse på alle de avgjørende attributtene. Ved negativ klassifikasjon er jobben enklere. Her trenger vi kun å identifisere et avgjørende attributt negativt. Dersom vi finner at et objekt mangler et av de avgjørende attributtene trenger vi ikke undersøke de resterende. Objektet er eliminert fra entitetsklassen.
Eksempel:
La oss tenke oss entitetsklassen "UFO". For å være en UFO må objektet
ha to attributter:
1. Det må være flyvende
2. Det må være uidentifisert
Dersom jeg ser et fly, høyt på himmelen er det en UFO?
Attributt 1 flyvende bekreftes positivt.
Attributt 2 uidentifisert bekreftes positivt.
Svar: ja, jeg har sett en UFO.
Denne konklusjon kan diskuteres, dens riktighet vil avhenge av innholdet av de begrepene som beskriver attributtene. Derfor er det viktig at disse er klart og entydig definert, ellers blir klassifikasjonen subjektiv og tilfeldig.
Dersom jeg sparker fotballen min høyt over mål, er den da en UFO?
Attributt 2 uidentifisert bekreftes
negativt. Objektet er identifisert.
Vi trenger ikke å sjekke attributt 1, vi har en negativ klassifikasjon.
Attributter er ikke nødvendigvis absolutte. Et attributt kan ha et sett med verdier, eller en verdiskala (kvantifisering). Seleksjon mellom entiteter gjøres ved hjelp av attributtverdier.
La oss tenke oss entitetsklassen "person".
En person kan ha disse attributtene:
- Navn
- adresse
- kommune
- fødsel/personnummer
- høyde
- vekt
- rase
- yrke
- sivil stand
Hvert av disse attributtene har verdier. I dette tilfellet har vi også attributter som direkte identifiserer det spesifikke objekt. Det er fødsels/personnummeret. For at et enkelt attributt skal kunne identifisere en enkel entitet må den ha en unik verdi for hver entitet som inngår i klassen. Ved hjelp av slike attributter kan vi altså selektere ut enkeltelementer fra en mengde. Vi kan også tenke oss at et sett av attributter kan fungere som unik identifikasjon. F.eks. kan vi splitte fødsels/personnummer opp i to attributter. Seleksjon på andre attributter, eller kombinasjoner av attributter vil gi meg delmengder som svar. Jeg kan f.eks. selektere ut alle personer som har sivil stand = ugift. Slike betingelser av kombinasjoner for seleksjon av en delmengde fra en mengde kan beskrives logisk, ved hjelp av vanlige logiske uttrykk. Dette kan beskrives symbolsk på mange måter. Jeg har valgt å kombinere boolske symboler med mengde symboler:
Delmengde = hovedmengde | logisk uttrykk
Eksempel:
Vi skal nå selektere fra entitetsklassen "person". Vi bruker følgende
logiske variabler:
a = (Høyde > 180 cm)
b = (sivil stand = "gift")
c = (rase = «kineser»)
d = (rase = «indianer»)
Mengden P er entitetsklassen «person»
Vi vil selektere ut en mengde X, som inneholder alle personer som er over 1.80 høy, er gift og er kineser eller indianer. Dette kan logisk beskrives slik:
X = P | a * b * (c + d)
Vi kan godt tenke oss å bruke mengde-operatorer i slike uttrykk, men de kan gjøres overflødige. Et av attributtene for en entitet kan nemlig være hvilket sett av mengder entiteten tilhører. Dersom vi gir elementene fra mengdelæren et attributt, nemlig mengdesett, kan sammenhengen mellom mengdelæren og entitetslæren greit vises:
Vi tenker oss følgende logiske variabler:
a = (mengdesett inneholder A) (er et
element i bl.a. i mengden A)
b = (mengdesett = inneholder B)
Mengden C inneholder alle elementer fra A og B:
Vi får da følgende sammenheng:
|
Union |
X= A u B |
X = C|a+b |
|
Snitt |
X = A s B |
X = C|a*b |
|
Differens |
X = A \ B |
X = C|a*(-b) |
I mengdelæren er det en kombinasjonsmulighet som mangler, nemlig:
X = C | (a * (-b)) + (b * (-a))
Denne kombinasjonsmuligheten er motsatt av snitt. I boolsk terminologi kalles denne kombinasjonen for "eksklusiv eller". I god tradisjon kan vi likegodt kalle denne funksjonen for «eksklusiv union».
Funksjonen er en slags union som ekskluderer de elementer som har mengdesett = {A,B}, altså som både er i A og B.
For å kunne bli en komplett modell av verden, må entitetene også kunne ha relasjoner mellom seg. Det finnes fysiske og logiske relasjoner. Logiske relasjoner kan f.eks. være eierforhold, kontrakt, slektskap osv. Fysiske relasjoner er berøring, og kan selvfølgelig kun eksistere mellom fysiske entiteter. Eksempler på slike relasjoner kan være:
En mann som hører til entitetsklassen "person" eier en bil som hører til entitetsklassen "bil". Mannen kan ha barn som også hører til "person".
I og med at datamaskiner mer og mer blir tatt i bruk til informasjonshandtering er behovet for formelle måter å beskrive deler av virkeligheten på øket sterkt. Teorien om entiteter, relasjoner og attributter er et utspring av dette behovet. Det har f.eks. vist seg at det ikke er noen enkel oppgave å organisere relasjonene slik at en database fungerer mest mulig effektivt. Men ut av dette havet av nytenkning kommer en mengde generelle teorier som greit lar seg anvende på andre områder enn bare i EDB-verdenen. Det er snakk om å se verden med nye øyne.
Slutning fra det generelle til det spesielle kalles for en deduktiv slutning. Deduktive slutninger bygger på at gitte premisser er sanne, ut fra disse premissene utleder man en nødvendig konklusjon. Dersom slutningen er logisk riktig og premissene er sanne blir konklusjonen sann. Eksempel:
|
Premiss 1 |
Alle fisker har gjeller |
|
Premiss 2 |
Sild er en fisk |
|
Konklusjon |
Sild har gjeller |
Dersom det er sant at alle fisker har gjeller og at sild er en fisk kan vi med full sikkerhet trekke den konklusjonen at sild må ha gjeller.
|
Premiss 1 |
Alle mennesker har vinger |
|
Premiss 2 |
Per er et menneske |
|
Konklusjon |
Per har vinger |
Denne siste konklusjonen er like gyldig som den første. Vi vet at den ikke er sann, det er fordi en av premissene er feil. Nå skal ikke vi inn på slutnings-teorien her, men bare poengtere at deduksjon er et av vitenskapens viktigste redskaper for å svekke, avkrefte eller styrke hypoteser. Ut fra en hypotese kan man dedusere dens nødvendige følger. Dette gir muligheter for å ettersjekke disse konklusjonene ad empirisk vei; ved hjelp av erfaring (eksperimenter og undersøkelser).
Forut for deduksjonen har der som regel foregått en hypotesedannelse eller en abduksjon, eller det kan være en ren induksjon man ønsker å ettersjekke.
La oss først se på hva en induksjon egentlig er. En induksjon er egentlig det motsatte av en deduksjon; det er en slutning fra det spesielle til det generelle.
Eksempel
Jeg har hittil ikke truffet kvinner som har den store sansen for programmering.
Ut fra dette er det nærliggende og slutte at kvinner generelt ikke har
den store sans for programmering. Men hvor sikker er en slik slutning? Hvor
mange promille av alle verdens kvinner har jeg truffet? En forsvinnende liten
del. Det er jo slett ikke sikkert at jeg enda har truffet gjennomsnittskvinnen
på dette området. Ut fra mitt spede erfaringsmateriale er dette en høyst
usikker slutning.
Dette er en svakhet som gjelder generelt for alle induktive slutninger. De er bare sannsynlige. Men sannsynligheten øker med undersøkelsesmaterialet. Hver eneste gang jeg legger en tørr tregjenstand i vannet flyter den. Jeg har aldri hørt om at noen har erfart noe annet. Det kan lede meg til å formulere loven: Alt tørt tre flyter. For hver gang jeg prøver, og treet flyter øker sannsynligheten for at denne loven medfører riktighet. Med utgangspunkt i denne loven kan jeg nå gjøre deduktive slutninger. Kork er tre. Alt tre flyter. Konklusjon: kork flyter. Jeg kan sjekke det ved å hive kork på vannet. Korken flyter. Igjen styrkes min hypotese om at alt tre flyter. Men merk: den bevises ikke. Det kan være at neste gang jeg prøver synker korken.
Abduksjon innebærer et forsøk på å forklare et eiendommelig eller uventet fenomen ved hjelp av å anta eksistensen av noe annet. Grunnene som anføres sannsynliggjør slutningen i en viss grad. Bevis for hypotesen får man først idet det antatt eksisterte blir bekreftet. Et eksempel på en slik slutning kan være oppdagelsen av lysets bølge-natur. Man oppdaget tidlig at lyset viste interferens-egenskaper som bare bølger kan ha. Dette ledet til den antagelsen at lyset var bølger. Men ifølge klassisk fysikk måtte bølgene ha et medium å spre seg i. Dermed oppstod hypotesen om den såkalte "eteren". Det ble gjort iherdige forsøk på å påvise eksistensen av denne, men alle disse har mislyktes. I dag regnes denne hypotesen for å være feil.
Et annet eksempel på abduksjon er hvordan Adams og Leverrier kom til å anta eksistensen av en planet utenfor Uranus:
Uranus bane viste eiendommelige uregelmessigheter som ikke lar seg forklare ut fra hittil kjente fakta og lover.
Hvis der fantes en planet med en bestemt masse utenfor Uranus, ville den etter kjente lover frembringe disse uregelmessighetene i Uranus bane.
Ingen andre forklaringer på dette fenomenet fantes.
Konklusjonen var at der måtte finne en planet utenfor Uranus bane.
Denne hypotesen ble senere bekreftet, da man oppdaget Pluto. Dermed ble det vitenskapelig bevist at hypotesen var sann; gjetningen var riktig. Men vi skal merke oss at det til syvende og sist alltid blir det empirisk erkjente som blir avgjørende for hypotesens sannhetsverdi. Erfaringen står over fornuften.
Tankenødvendige slutninger er slutninger uten indre selvmotsigelse. Hva er så en selvmotsigelse? Svaret på det gav Aristoteles i sitt berømte selvmotsigelses-prinsipp (Kontradiksjons-prinsippet):
«Det er umulig at det samme både kan tilkomme og ikke tilkomme det samme med hensyn til det samme på samme tid»
Hvordan vet vi at dette er sant? Dette er en av logikkens viktigste forutsetninger. Vi kan i alle fall si at i den verden vi opplever slår dette ikke feil. Men kanskje har også en slik fundamental påstand sitt gyldighetsområde. I kvanteteorien er nemlig et slikt prinsipp ikke så sikkert lengre.
Alle tankelogiske bygninger starter med en del grunnforutsetninger, og regler for hvordan disse kan anvendes. Den videre oppbygningen beslår i å trekke konklusjoner som følger av disser reglene og forutsetningene. Dersom en konklusjon er trukket uten brudd på reglene er den motsigelsesfri. I motsatt fall har vi en selvmotsigelse. En selvmotsigelse er ikke nødvendigvis det samme som flertydighet. Flertydigheter er en følge av at det samme regelsett gir mulighet for flere svar på samme spørsmål. I slike tilfeller er regelsettet ikke presist nok. Ligningen X^2 = 4 gir mulighet for flere svar. Vi har likevel ingen selvmotsigelse. Jeg velger å definere en selvmotsigelse slik:
1. Et regelsett som gir tvetydig svar og hvor disse svarene benekter hverandre
2. Et regelsett som gir inntrykk av å gi flere mulige svar, men som alltid gir samme svar uansett inngangsdata.
Begge disse tilfellene inneholder, som vi skal se, et brudd på selvmotsigelses-prinsippet.
Eksempel på 1:
A + B = C ==> A = B
A + B = C ==> A <> B
Disse reglene kan ikke brukes sammen fordi de benekter hverandre. Regelsettet er selvmotsigende.
Eksempel på 2:
For å være speider må du være medlem av avholdsforbundet og av idrettslaget. (S
= A * I)
For å være medlem av avholdsforbundet må du aldri nyte alkohol. (A = (-N))
For å være medlem av idrettslaget må du være aktiv i minst en idrett og du må
delta i idrettslagets fester. ( I = ID * F)
For å kunne delta i idrettlagets fester må du kunne nyte alkohol (F = N )
Dette regelsettet gir inntrykk av at det må gå an å være speider, og at det går an og ikke være speider. Men, som alle har sett, det er umulig å bli speider.
S = A * I
S = (-N) * (ID * F)
S = (-N) * (ID * N)
S = (-N) * ID * N = ID * (N * (-N)) = ID * 0 = 0
Dersom mengden av potensielle speiderkandidater
er X og mengden av speidere er Y får vi:
Y = X | S = 0 (den tomme mengde)
Ingen potensielle speiderkandidater kvalifiserer til å bli speidere. Dette på grunn av indre selvmotsigelser i det regelsettet som spesifiserte kravene til en speider.
En slik selvmotsigelse kan også føre til det motsatte, nemlig at alle inngangskombinasjoner vil gjøre svaret sant. Selvmotsigelsene følger direkte av de boolske regnereglene:
X * (-X) = 0 og
X + (-X) = 1
Slik som jeg har definert det vil altså enhver selvmotsigelse inneholde en påstand og en benektelse av det samme, altså en kontradiksjon. Hva som er påstand og hva som er benektelse kommer an på sammenhengen. Forholdet er komplementært. Det kan sammenlignes med Newtons 3 lov om at enhver kraft må ha en motkraft som er like stor men motsatt rettet. Dersom vi skal ha en selvmotsigelse må vi ha to komplementære påstander. Altså en påstand og en benektelse av den samme påstanden.
Selvmotsigelser kan deles i to grupper:
1. Indre selvmotsigelser
2. Ytre selvmotsigelse
En indre selvmotsigelse har vi når hele selvmotsigelsen finnes innenfor den presenterte enhet. Den presenterte enhet kan være en setning, en hypotese, en teori, et dogme osv. presentert som en helhet. Men en slik presentert enhet hevdes som regel å stå i en større sammenheng. Den er en del av en større helhet. Enhetens sammenheng med helheten blir ofte bare overfladisk skissert. Dersom selvmotsigelsen inne holder en påstand og det komplementære motstykke befinner seg uten for enheten men innenfor den større helheten, har vi en ytre selvmotsigelse. Ytre selvmotsigelser er vanskelige å oppdage. Men ved hjelp av dogmematrisemetoden kan man gå systematisk til verks for å finne selvmotsigelser. Dogmematrisemetoden er meget enkel men den krever mye arbeid. For store teorier og hele religioner er den uoverkommelig. Metoden går ut på å bryte en teori ned i mindre enheter. Disse enhetene nummereres og settes opp i en matrise. Deretter blir 1, sjekket mot 1, og mot 2, 3, 4, 5 osv. Så blir 2, sjekket mot 2, 3, 4, 5 osv. På denne måten krysseksamineres teorien systematisk. Men denne krysningen kan bli komplisert. For å avdekke selvmotsigelser må man kanskje bryte hver enhet ned i enda mindre detaljer, også disse detaljene må sjekkes mot seg selv og mot den andre enhetens detaljer. Når vi sjekker detaljene mot seg selv, bruker vi dogmematrisen på vanlig måte, men nå på en mindre enhet. Når vi skal sjekke en enhets detaljer mot en annens, utgjør hver av enhetenes detaljer en dimisjon i matrisen.
For å klargjøre dette tar jeg et eksempel. Vi tenker oss vitenskapens verdensbilde inndelt i følgende teorier:
1. Big Bang (BB)
2. Solsystemets utvikling (SU)
3. Jordens geologiske utvikling (JU)
4. Livets begynnelse (LB)
5. Evolusjonsteorien (E)
Dette er satt opp i matrisen under:
|
|
1 BB |
2 SU |
|
1 BB |
1,1 |
1,2 |
|
2 SU |
2,1 |
2,2 |
|
3 JU |
3,1 |
3,2 |
|
4 LB |
4,1 |
4,2 |
|
5 E |
5,1 |
5,2 |
|
|
3 JU |
4 LB |
5 E |
|
1 BB |
1,3 |
1,4 |
1,5 |
|
2 SU |
2,3 |
2,4 |
2,5 |
|
3 JU |
3,3 |
3,4 |
3,5 |
|
4 LB |
4,3 |
4,4 |
4,5 |
|
5 E |
5,3 |
5,4 |
5,5 |
Så kan vi spørre oss selv:
Er Big bang forenelig med seg selv (1,1)?
Er Big bang forenelig med solsystemets utvikling (1,2)?
Er Big bang forenelig med jordens geologiske utvikling (1,3)?
Osv.
Disse spørsmålene lar seg som regel ikke
besvare før teoriene er brutt videre ned i underteorier.
Underteorier for Big bang kan f.eks. være:
1.1 Stjerners utvikling (SU)
1.2 Galaksers utvikling (GU)
1.3 Klassisk fysikk (KF)
1.4 Kvantefysikk (KV)
1.5 Astronomi (A)
1.6 Relativitetsteorien (R)
Underteorier for livets begynnelse kan være:
4.1 Kjemi (Kj)
4.2 Fysikk (Fy)
4.3 Biokjemi (BK)
4.4 Genetikk (G)
For å sjekke Big bang mot seg selv setter vi den opp i en ny dogmematrise. Stemmer f.eks. astronomiske tolkningen av astronomiske observasjoner med relativitetsteorien? Hva med observasjoner som antyder at galakser har en hastighet bort fra oss som er større enn lyshastigheten?
En slik tabell er vist under og vi begynner å få en antydning av problemets store omfang.
|
|
1 SU |
2 GU |
3 KF |
|
1 SU |
1,1 |
1,2 |
1,3 |
|
2 GU |
2,1 |
2,2 |
2,3 |
|
3 KF |
3,1 |
3,2 |
3,3 |
|
4 Kv |
4,1 |
4,2 |
4,3 |
|
5 A |
5,1 |
5,2 |
5,3 |
|
6 R |
6,1 |
6,2 |
6,3 |
|
|
4 KV |
5 A |
6 R |
|
1 SU |
1,4 |
1,5 |
1,6 |
|
2 GU |
2,4 |
2,5 |
2,6 |
|
3 KF |
3,4 |
3,5 |
3,6 |
|
4 Kv |
4,4 |
4,5 |
4,6 |
|
5 A |
5,4 |
5,5 |
5,6 |
|
6 R |
6,4 |
6,5 |
6,6 |
Når vi skal sjekke Big Bangs detaljer mot detaljer som inngår i livets begynnelse kan vi sette opp en matrise som vist i tabellen under:
|
|
1 Kj |
2 Fy |
3 BK |
4 G |
|
1 SU |
1,1 |
1,2 |
1,3 |
1,4 |
|
2 GU |
2,1 |
2,2 |
2,3 |
2,4 |
|
3 KF |
3,1 |
3,2 |
3,3 |
3,4 |
|
4 Kv |
4,1 |
4,2 |
4,3 |
4,4 |
|
5 A |
5,1 |
5,2 |
5,3 |
5,4 |
|
6 R |
6,1 |
6,2 |
6,3 |
6,4 |
Når det gjelder vitenskapelige teorier kommer vi som regel til syvende og sist inn på felles teorier, eller disipliner: fysikk, kjemi, og matematikk. Vitenskapsmennenes store drøm er å forene eller tilbakeføre alle vitenskapelige teorier til en eneste disiplin beskrevet ved hjelp av matematikk. På denne måten ville man være garantert fri for selvmotsigelser dersom matematikken selv er fri for selvmotsigelser.
Når en teori er fri for indre selvmotsigelser sier vi at den er konsistent. En slik teori kan ofte være et vakkert logisk byggverk som man lett blir fasinert av. Av og til gjør man den feilen at man, på grunn av teoriens klare logikk, oppfatter den som nødvendig sann. Euklids geometri er et slikt byggverk. Lenge hadde man den oppfatning at Euklids geometri var den eneste måten å beskrive rommet på. Immanuel Kant så på Euklids geometri som «syntetisk apriori sannhet» Det er en sannhet som man kan erkjenne om virkeligheten uten å erfare den. Euklids geometri danner grunnlaget for Kants syn på matematikken, nemlig at matematikken forteller oss sannheter om virkeligheten, som ikke trenger bekreftelse gjennom erfaring. Bertrand Russell avviser Kants syn på matematikken. Den symbolske logikks fremskritt, gjør det nå mulig å forkaste denne delen av den kantske filosofi. Fremveksten av såkalte ikke-euklidske geometrier har gjort det klart at ren matematikk ikke tar hensyn til spørsmålet om Euklids aksiomer og læresetninger gjelder for det faktiske rom, eller ikke. Utviklingen av ikke-euklidske geometrier har sammenheng med erstatninger av Euklids femte postulat. I sammenheng med de andre fire postulatene virker det femte ganske innviklet og det har vært gjort flere forsøk på å bevise det femte postulat ved hjelp av de fire andre, men ingen har lykkes. Euklids femte postulat sier kort at dersom to rette linjer ikke er parallelle vil de før eller siden møtes, når de trekkes ut i det uendelige. Måten å avgjøre ikke-parallellitet på er å trekke en tredje linje som skjærer de to andre. Dersom summen av vinklene som denne linjen danner med de to andre linjene er ulik summen av to rette er linjene ikke parallelle. Linjene vil skjære hverandre på den siden hvor summen av vinklene er mindre enn 180 grader. Da denne setningen ikke følger av de fire andre kan vi like godt erstatte dette postulatet med andre som er i strid med dette. Det er derfor mulig å lage konsistente geometrier på grunnlag av nye defineringer av dette postulatet. Den tyske matematikeren Bernard Riemann erstattet Euklids 5 postulat med følgende:
Gitt en rett linje og et punkt utenfor denne linje, kan det ikke trekkes noen linje gjennom det gitte punkt som ikke skjærer denne linjen.
Det finnes m.a.o. ingen parallelle linjer. I den riemannske geometri er summen av vinklene i en trekant alltid større enn to rette.
Den russiske matematiker Nikolaj Lobatsjevskij erstattet postulatet med et som hevdet at alle linjer er parallelle, i den forstand at de aldri ville møtes. Det kreves fantasi for å tenke seg noe slikt. Men det er intet i logikken som foretrekker det ene fremfor det andre. Det er bare vanetenkning som gjør at vi foretrekker det Euklidske postulatet. De ikke-euklidske geometrier er like logisk motsigelsesfrie som den euklidske. De er alle konsistente. Formelt logisk er det derfor ingen grunn til å foretrekke den ene geometrien fremfor den andre.
Hva ville så Kant ha svart til dette? Hans standpunkt måtte bli noe i retning av at, riktignok er alle geometrier likeverdige som rene aksiomatiske systemer, men likevel er det bare den euklidske som gir en sann beskrivelse av det virkelige rommet.
Men er dette egentlig sant? Einsteins relativitetsteori har endret det klassiske synet på rommet. Ifølge denne teorien vil summen av vinklene i en trekant, under gitte betingelser, være større enn 180 grader, dvs. det ville stemme med den riermannske geometri. Denne oppfatningen avhenger av hvordan vi vil definere en rett linje. Dersom vi benytter en vanlig definisjon, nemlig at en rett linje er den banen lyset følger, vil vi måtte benytte den riemannske geometrien for å beskrive et rom som er krummet av gravitasjonen. Andre definisjoner på den rette linje fører til at vi likevel må ty til den euklidske geometrien. Det er her Kant, ifølge Bertrand Russell, har gått seg vill. Han regnet med Euklidsk geometri som den eneste mulige måten å beskrive rommet på. Russell så på matematikken som en rent formal vitenskap. Den tar ikke hensyn til hva som er virkelighet, og virkelighet kan ikke erkjennes gjennom matematikken. Vi kan altså teoretisk utvikle så mange aksiomatiske systemer vi bare vil. Dersom de aksiomer og de regler / lover systemet består av, kan overføres på virkeligheten har vi funnet en matematisk / logisk modell som fungerer som beskrivelse av en del av virkeligheten. Men vi må skille klart mellom modell og virkelighet. Modellen er ikke virkelighet. Vi kan godt tenke oss at andre modeller kan beskrive den samme virkeligheten like bra som den første. Jo mer kompleks virkelighet vi prøver å beskrive, jo flere modeller kan vi bruke til å beskrive de samme fenomener. En slik konsistent modell som er egnet til å beskrive en del av virkeligheten, kalles en hypotese, i tillegg har jeg kalt den for en lukket forklarings-modell. Den er lukket i den forstand at vi ikke trenger mere enn den modellen for å beskrive et område av virkeligheten. Men en slik lukkethet kan ofte narre folk til å tro at det ikke er mulig å se det hele på en annen måte.
Gitt et sett av fenomener. En konsistent modell av aksiomer og lover setter disse fenomenene i sammenheng og gir en rimelig forklaring på dem. Har jeg da et bevis på at modellen er sann? Kan jeg i så fall bruke fenomenene til å bevise postulatene? Dersom det ikke finnes noen alternativer til denne modellen kan vi regne sannsynligheten som stor for at den er sann. Men, la oss si at jeg kan stille opp en alternativ modell, som bygger på et annet sett av postulater, som strider mot de første. Hva blir konsekvensen? Jo nå har hver av modellene en sannsynlighet på maks 50 % Det er heller ikke utenkelig at det kan komme opp en tredje modell. Hvilken garanti har vi for at det ikke en gang i fremtiden kan komme opp alternative modeller f.eks. til Big Bang. Selv om denne modellen henger logisk sammen, og selv om den forklarer mye, kan vi ikke vite at den er sann kun med utgangspunkt i at dens indre logikk er konsistent. Det finnes forresten alternativer til Big bang. (f.eks. teorien om materie og antimaterie).
Hypoteser kan imidlertid styrkes, svekkes eller avkreftes ved å utlede de konsekvenser de måtte føre til og deretter etter-sjekke disse ved hjelp av eksperimenter. Dette er den vitenskapelige metode.
Oppsummering:
1. En lukket forklaringsmodell er ikke nødvendigvis sann selv om den er konsistent og stemmer med fenomener.
2. Vi kan ikke bevise postulatene i en lukket forklaringsmodell ved å henvise til fenomenene (induktiv slutning).
3. En lukket forklaringsmodell kan styrkes, svekkes og kanskje avkreftes, men den kan aldri bekreftes.
4. En lukket forklaringsmodell som ikke er falsifiserbar er uvitenskapelig.
5. Lukkede forklaringsmodeller kan ofte ha høy forklaringskraft, uten at dette beviser noe som helst.
Hvordan er forholdet mellom forklaring og beskrivelse? Er det å forklare det samme som å beskrive? Det kommer an på. Dersom vi måler hastigheten til et legeme i fall på forskjellige punkter, kan resultatene forklares ved hjelp av Newtons gravitasjonslov. Men forklarte Newton egentlig hva gravitasjonen var? Nei, han forklarte bare hvordan den virket. Newton bygget en modell som beskrev tyngdeloven. Men den sier ingenting om hvorfor den er slik. Den dag i dag har vi ikke kommet til bunns i hva tyngde egentlig er. Spørsmålet er om vi noensinne kommer helt til bunns i slike spørsmål. Selv om vi lyktes å forklare tyngdeloven ved hjelp av andre mer generelle lover, ville vi bare ha forskjøvet problemet, for hva er forklaringen på disse lovene? osv. Vi ender altså opp med spørsmålet om forklaringen på tilværelsen? Kanskje ligger det langt utenfor vår rekkevidde, kanskje finnes det ingen slik forklaring.
En lukket eksistensial modell er et spesialtilfelle av en lukket forklaringsmodell. Forskjellen er at:
1) Modellen er ikke falsifiserbar
2) Den har ubegrenset forklaringskraft (et lukket postulat)
3) Den er altomfattende
Du har sikkert møtt personer som har en forklaring på alt. Ingen fenomener, ingen mysterier, eller problemer gjør ham svar skyldig. Han har en teori som er så generell at den favner alt. Vi mennesker har alltid søkt etter svar på de eksistensielle spørsmål. Hvor kommer vi fra? Hva er meningen med livet? Hvor går vi hen? osv. For mange av oss er det uutholdelig, ikke å kjenne løsningen. Erkjennelsesteorien indikerer imidlertid det harde faktum at vi fortsatt er langt fra noe sikkert svar på slike spørsmål. Alle har vi en eller annen forestilling om den virkelighet som omgir oss. Inne i hodet vårt har vi bygd opp en modell av virkeligheten. Denne modellen er konstruert på grunnlag av de erfaringer vi har mottatt igjennom våre sanser. Nye erfaringer blir plassert der de hører hjemme i denne modellen. Alle erfaringer som enkelt passer inn i modellen er med på å bekrefte den. Nå er det slik at vi fra tid til annen blir konfrontert med erfaringer som ikke passer inn. Når vi blir konfrontert med ukjente fenomener leter vi alltid etter en forklaring. Vi lager oss teorier. Disse teoriene blir ofte satt i sammenheng med de eksistensielle spørsmål. Vi bygger altså ut vår modell av virkeligheten med teorier som omfatter det unormale og det uforklarlige. Dette gjør vi alle sammen til en hvis grad. Dersom vi er flinke og konstruerer en teori som kan forklare alt, har vi to muligheter:
1. Vi har funnet sannheten
2. Vi har konstruert en Lukket Eksistensial-Modell (LEM)
Jeg tror at svært mange av oss ikke er helt klar over den siste muligheten, og det kan gjøre oss temmelig blind.
LEM kan alltid identifiseres ved at den har en eller flere lukkende postulater. Et lukket postulat har som sagt den egenskapen at det forklarer alt. Det lukker hele tilværelsen inn i en stor modell. Et postulat er en påstand. Men et lukket postulat er ingen vanlig påstand, det knytter seg spesielle egenskaper til en slik påstand. Den er nemlig forenelig med hvilket som helst saksforhold. Det går altså ikke an å avgjøre påstandens sannhetsverdi ved å henvise til et bestemt saksforhold. Man kan derfor spørre om de egentlig er påstander. La oss se på noen eksempler:
«Det sitter en katt på trappa»
Dette er en normal påstand. Sannhetsverdien kan avgjøres ved å sjekke om det virkelig sitter en katt på trappen.
«Dinosaurene døde ut som følge av et meteornedslag for 65 millioner år siden»
Denne påstanden er vanskeligere å sjekke, men ved å grave og forske kan vi iallfall få indikasjoner for og imot påstanden.
«Gud er i alle ting»
Dette er en typisk ugjendrivelig påstand. Jeg kan selvfølgelig åpne et egg og si at Gud var ikke der. Men da er selvfølgelig svaret at Gud ikke kan oppfattes med sansene, så han var i egget likevel. Dette kan aldri gjendrives ved hjelp av noe saksforhold. Det er en uangripelig påstand.
«Universet[2] er uendelig»
Hvordan i all verden skal vi få sjekket det? Uansett hvor mye vi kunne observere, kan vi ikke si at vi har sett uendeligheten. Er påstanden sann, kan den ikke bevises.
Det lukkede postulat må ha slike egenskaper for at det skal kunne fungere. Men likevel blir det begrunnet nettopp ved hjelp av avgrensede saksforhold. Dette ender som regel opp i avanserte sirkel begrunnelser. Man starter med et sett uforklarlige fenomener. Ut fra disse kommer man med en teori som gir forklaring på fenomenene. Deretter blir fenomenene brukt som bevis på at teorien er riktig. Dette er samme type feil som var nevnt i forrige avsnitt, nemlig at fenomener blir anvendt for å bevise postulater. En LEM forklarer ikke bare et delsett av fenomener, den forklarer alle, absolutt alt i hele verden. Vi får en følelse av å ha den helt store oversikten. Jeg tror at en slik teori må ha en viss kompleksitet for at vi mennesker skal bli fenget av den, men det er ingenting i veien for å konstruere en meget enkel en:
Det var en gang en julenisse som var ensom og hadde ingen steder å bo. Denne nissen var veldig flink å lage julegaver. Den første julegaven han lagde var til seg selv, det var en stor rund kule som han kunne bo på. Den kalte han "jorden". Deretter lagde han en masse folk som han kunne gi gaver til. Den første julen fikk de dyr, trær, blomster, sol, måne osv. Deretter ble det mange juler og folk var lykkelige og fikk mange gaver. Men julenissen var ensom når det ikke var jul, derfor bestemte han seg for at menneskene skulle bli julenisser. Dette blir de når de dør. Da skal vi holde den store julenissen med selskap hele året. Men for at vi skulle kunne bli julenisser må vi formes som mennesker. Dette skjer igjennom de prøvelser og lidelser vi gjennomgår på livets vei.
Dette er en enkel modell som alle lett gjennomskuer. Ikke desto mindre kan jeg ved hjelp av denne modellen forklare hele tilværelsen. Jeg vet hvor jeg kommer fra, jeg vet hvor jeg går, jeg vet hvorfor jeg er her, jeg kan forklare det onde og det godes problem. Kort sagt modellen er den hele og fulle forklaring på hele tilværelsen.
Hva er den lukkende faktor her? Jo selvfølgelig, vi har jo bare en faktor og velge i og det er selve julenissen, men er han den eneste faktor? Hvis nå jeg våger og stille følgende kritiske spørsmål: Hvor kommer julenissen fra? Dette er et spørsmål som modellen ikke gir svar på. Dette spørsmålet kan vi håndtere på to måter:
1. Vi kan vri oss unna det:
a. Dette er julenissens store hemmelighet, det skal ikke du bry deg med (retorikk og hersketeknikk)
b. Med hvilken rett stiller du slike spørsmål om selveste julenissen? (Autoritet)
c. Det vet hverken vi eller julenissen
2. Vi kan innføre et nytt postulat, som utvider den primære lukkende faktor:
a. Julenissen har alltid eksistert, eller
b. Julenissen hadde makt til å skape seg selv.
Det er ikke vanskelig å oppdage likhetstrekkene mellom en slik modell og religioner som f.eks. jødedommen og islam. Modellen bringer derfor ikke noen fundamentale nye ideer. Vi har jo stort sett bare erstattet Gud med Julenissen. Dette er gjort med hensikt, slik at modellen skal være enkel å gjennomskue. Vi må huske på at andre religioner som bygger på de samme postulater, har utviklet seg gjennom mange generasjoner. Derfor er de mye mer sofistikerte. De grunnleggende postulater er nesten abstrahert bort. Religionene blir komplekse, og det er nettopp det vi mennesker så lett faller for.
Men går det an å lage en LEM som er grunnleggende forskjellig fra religionene? Det er dette vår tids vitenskap prøver å gjøre, vha. teorier som big-bang og evolusjonen. Men dette er åpne modeller, som kun forsøker å forklare avgrensede områder av tilværelsen.
I logikken skilles det klart mellom to typer formuleringer:
1. De analytiske
2. De syntetiske
En formulering består av a) logiske ord og b) begreper. Det er begrepene som gir setningen et innhold som forbinder den med et saksforhold. Begrepene omfatter også språkbruksregler som kan være avgjørende for hvilken type setning vi har med å gjøre.
De logiske ord gir setningen dens logiske form, eller struktur. Vi har tidligere nevnt noen logiske ord: «og», «eller», «ikke», «alle», «noen» osv. Av og til kan det være vrient å skille mellom form og innhold; mellom logiske ord og begreper. Analytiske formuleringer er formuleringer hvor vi, ut fra formuleringens logiske form og språkbruksregler, kan avgjøre sannhetsverdien. Av dette følger det naturlig at vi har to typer analytiske formuleringer, nemlig de usanne og de sanne. De usanne kaller vi for negativt analytiske formuleringer og de sanne kalles for positivt analytiske formuleringer.
Her er definisjonen på en negativt analytisk formulering:
Med «en negativt analytisk formulering» skal vi forstå «en formulering som enten er logisk feilaktig eller som blir til en logisk feilaktig formulering ved anvendelse av definisjoner for de ikke-logiske uttrykkene som inngår i den.»[1]
Hvordan skal vi så kunne avgjøre om en formulering er logisk feilaktig? Jo, her bygger vi på kontradiksjons-prinsippet, eller Aristoteles motsigelses-prinsipp. Symbolsk kan det fremstilles slik:
A * -A (A og ikke-A)
Eks: Det er umulig at en person kan være død og ikke død på samme tid. Hvis vi tenker oss utsagnet:
Jensen er død og ikke død.
Her kan vi erstatte de ikke-logiske ordene med store bokstaver
da får vi:
A er B * - B
Her gjenkjenner vi straks formen for en kontradiksjon; en selvmotsigelse, følgelig er formuleringen negativt analytisk.
Alle former hvor kontradiksjonsprinsippet kan identifiseres er alltid logisk usanne. Her er eksempler på et par andre former:
Noen A er ikke A.
Noen A som er B er ikke B.
Med "en positivt analytisk formulering" skal vi her forstå "en formulering som enten er logisk sann eller som blir logisk en logisk sann formulering ved anvendelse av definisjoner for de ikke-logiske uttrykkene som inngår i den."
Her er en positivt analytisk formulering:
Enten var jeg på jobb kl 12 i går eller jeg var ikke på jobb kl 12 i går
Reduseres til:
Enten A eller ikke A
Reduseres til
A + - A
Utsagnet er alltid sant, fordi jeg ikke samtidig kan være på jobb og ikke på jobb (i alle fall med vanlig forståelse av begrepet "å være på jobb")
Her er noen andre klare former for positivt analytiske utsagn:
Hvis A så A. (A ==> A)
Hvis det er krig så er det krig
Alt som er A er A
Alt som er gammelt er gammelt
Alt som er A og B er B
Alt som er vakkert og skinnende er skinnende.
Vi skal merke oss at analytiske formuleringer sier ingenting om omverdenen. De gir oss ingen ny informasjon, som vi trenger å gjøre undersøkelser for å ettersjekke. Derfor er de også like sikre som de logiske forutsetninger vi legger til grunn for dem. Regner vi kontradiksjons-prinsippet som absolutt gyldig, er det mulig å avgjøre sannhetsverdien på slike utsagn med absolutt sikkerhet.
Vi skal også merke oss at definisjoner er analytiske utsagn.
Det vil si at de avgrenser eller forklarer begreper. "alle sirkler er runde" er et analytisk utsagn, fordi definisjonen på en sirkel sier at den skal være rund. Dersom den ikke er rund, er den ikke en sirkel. Vår forstand er enerådende når det gjelder å gi begreper innhold, derfor er slike utsagn absolutt sikre. De er sikre fordi de forklarer hva vi mener med begreper. Andre eksempler på analytiske utsagn: «Kobber er et metall» (så fremt det ligger i definisjonen på kobber at det skal være et metall). «Alle datamaskiner behandler data». «Alle ungkarer er ugift».
Definisjonen på en syntetisk formulering er enkelt og greit slik:
Med en syntetisk formulering skal vi forstå: En formulering som hverken er positivt eller negativt analytisk
Kan ikke sannhetsverdien avgjøres ved å studere formuleringens logiske form, sammen med definisjonene, er utsagnet syntetisk. Det betyr at sannhetsverdien kun kan finnes ved en undersøkelse av det saksforhold påstanden uttrykker. Eksempler på syntetiske formuleringer:
Det regner ute.
Katten sitter på trappen.
Torvald er flink å programmere.
Spania er en øy i Stillehavet.
Det siste ville kanskje noen reagere på. Det er fordi vi kjenner begrepene og det saksforhold de uttrykker så godt at vi vet at påstanden er feil. Men logisk sett er den ikke feil. Det er fullt mulig at Spania kunne vært en øy i Stillehavet. Den logiske formen er: A er B, og det er en gyldig logisk form, som kan være både riktig og gal alt etter hvilke begreper vi setter inn for A og B.
Tvils-tilfeller:
Hva med matematiske utsagn f.eks. geometriske og aritmetiske, er de syntetiske
eller er de analytiske. La oss ta f.eks. utsagnet:
2 + 2 = 4
Er det et analytisk eller et syntetisk utsagn? Kant argumenterte sterkt for at slike utsagn var syntetiske. Personlig er jeg ikke enig, men det kommer jeg tilbake til.
Forskjellen mellom kontradiksjon og kontrære begreper.
Det motsatte av liv er død. Liv og død er kontrære begreper; den utrykker motsetninger. Men liv og død er ikke en kontradiksjon. En kontradiksjon inneholder en påstand og en benektelse. Men benektelsen har ikke form av motsetning, men den er en ren negasjon av påstanden. Negasjonen av liv er ikke-liv. Det motsatte av død kan like godt være fødsel, så kontrære begreper er ikke entydige, det er derimot alltid kontradiksjonen.
Hva er egentlig tolkning? Vi møter denne aktiviteten i nesten alle livets forhold. Kanskje vi lettest kan finne ut av det ved å spørre hvorfor vi tolker. Vi lærer av IP-teorien at informasjon kun kan bli til ved hjelp av tolkning. En datastrøm er verdiløs uten at den blir tolket. Motivet for vår tolkning er at vi søker å oppfatte noe, eller å forstå noe. Det kan være fenomener, dyr, kunstverk, mennesker, tekster osv. Ut fra dette ser vi at tolkning omfatter en mengde aktiviteter som i seg selv er nokså forskjelligartede. Vi skal her se litt nærmere på dette med tekst-tolkning. Tekst-tolkning er utdyping og omforming, av en tekst, på en slik måte at budskapet i teksten blir fattbart for det enkelte individ. Nå skal vi ikke se på dette med tradisjonelle øyne, men vi skal fokusere på de problemstillinger vi står ovenfor når en tekst skal tolkes.
Det naturlige språk er kontekst-avhengig. Det betyr at ord og begreper ofte endrer innhold alt etter hvilken sammenheng eller kontekst de står i. Når vi ser et enkelt utsagn er det løsrevet fra konteksten, og da er det ofte vanskelig å gi en entydig tolkning av utsagnet. Innenfor vanlig tolknings-teori er det da vanlig å gi alternative mulige tolkninger som følger av de vanligst anvendte språkbruksregler som inngår i begrepet. Et utsagn kan lett endre seg fra analytisk til syntetisk eller motsatt alt etter hva vi legger i begrepene.
Eks:
Professoren er autoritær og gir rom for annerledestenkende.
Hva betyr det egentlig å være autoritær?
La oss her gi to mulige definisjoner:
1. Nekte å gi rom for annerledes tenkende
2. Å være personlig sikker.
Dersom vi substituerer formuleringen med 1 får vi et negativ analytisk utsagn. Substituerer vi den med 2 får vi et syntetisk utsagn. På samme måte kan et utsagn endre seg fra negativt til positivt analytisk ved å endre innholdet i begrepet.[2] Det betyr at den logiske kategori et utsagn har kan endre seg med begreps-innholdet. Den logiske form kan ikke endres, da denne er gitt av de logiske ordene (dersom disse er entydig forstått).
Enkelt-utsagn kan derfor uttrykke totalt forskjellige påstander alt etter hva man legger i begrepene. Vi skal ikke gå nærmere inn på tolkning av enkle utsagn her, men nøye oss med å konstatere at enkeltutsagn kan innebære utallige tolkningsmuligheter som, hver for seg, kan bety vidt forskjellige ting. Årsaken er begrepenes flertydighet.
Når vårt språk skaper så store vanskeligheter i kommunikasjonen, hvorfor setter vi oss ikke da det mål å konstruere det perfekte kontekstfrie språk? Et slikt språk måtte i så fall bestå av alle typer logiske ord, og entydig definerte begreper. Faktisk har mennesket gjennom tidens løp konstruert mange slike språk. De fleste av dem er blitt til i vårt eget århundre. Det er programmeringsspråkene. Men det matematiske språk, som er eldgammelt, har klare og veldefinerte begreper. Disse språkene har den klare fordel, at de minimaliserer muligheten for forvrenging av kommunikasjonen via begrepsforvirring. Men hvorfor henger vi fortsatt ved de gamle, naturlige språkene?
En optimalisering av begrepsklarheten i språket har dessverre en pris. Språket mister sin dynamikk; det blir uformelig. Det vil si at jo stivere språket blir, jo snevrere blir dets anvendelsesområde. Språket er der for at vi skal kunne beskrive den opplevde virkelighet. Men den opplevde virkelighet er full av nyanser og spesialtilfeller. Et stivt språk vil etterhvert miste bakkekontakten med virkeligheten. De fleste av oss har til tider opplevd, som i så glimt, sider av virkeligheten, som vi mangler ord for å beskrive. De religiøse opplevelser, og opplevelser under meditasjon er typiske områder hvor man stadig hører om maktesløshet når dette skal beskrives. Ellen G. White fikk et glimt inn i himmelen, her er hennes kommentar:
"Språket er alt for fattig til å kunne beskrive himmelen. Når jeg ser den for meg blir jeg stum av undring. Jeg gripes av den makeløse storheten og herligheten. Da legger jeg fra meg pennen og utbryter: 'Hvilken kjærlighet! Hvilken vidunderlig kjærlighet!' Selv det mest opphøyde språk mangler uttrykk til å beskrive himmelens herlighet og de ubeskrivelige dybder i Frelserens kjærlighet."[3]
En lignende parallell finner vi i uttalelser fra mystikerne. I sin meditasjon beveger de seg utover fornuftens domene og inn i den direkte opplevelse. Her er en uttalelse fra D.T. Suzuki:
"Den motsigelse, som er så forvirrende for vår alminnelige tenkemåte, skyldes det forhold, at vi er tvunget til å anvende språket for å vidregi vår indre erfaring, som ifølge selve sin natur unndrar seg språklig uttrykk."[4]
Østens filosofer er vel de som har sett dette problemet klarest, og innenfor mange retninger av Østens religioner legges det sterk vekt på metoder for på en måte å sette de språklige funksjoner ut av spill, da de bare forvirrer sinnet. En velkjent zen-aforisme lyder slik:
"I det samme øyeblikk du taler om en ting, skyter du forbi målet".[5]
Men dette gjelder ikke bare de underlige deler av vår psyke. Vitenskapsmenn har i vårt århundre blitt mer og mer i stand til å stille naturen stadig grundigere spørsmål. De svar, naturen gir, lar seg ikke beskrive i det naturlige språk. Den matematiske begrepsverden som kvanteteorien består av er så fjernt fra vår daglige opplevelse at vitenskapsmennene har store problemer med å bruke vårt alminnelige språk til å beskrive det. Når de anvender begreper som menigmann skjønner oppstår det paradokser og selvmotsigelser. Her er noen uttalelser fra en av kvanteteoriens grunnleggere, den tyske fysikeren og nobel-prisvinneren Werner Heisenberg:
"Språkproblemet er virkelig alvorlig. Vi ønsker å tale om atomenes oppbygging på en eller annen måte ... Men vi kan ikke tale om atomene i det alminnelige språk".
"Det vanskeligste problem ... vedrørende språkets anvendelse oppstår i forbindelse med kvanteteorien. Her har vi inntil videre ingen enkel ledetråd, for hvordan vi skal sammenholde de matematiske symboler med det alminnelige språks begreper; og det eneste sikre utgangspunkt, vi har, er den kjensgjerning at våre alminnelige begreper ikke kan anvendes på atomenes oppbygging".
Når vi mennesker fra tid til annen, enten via intens suggesjon av vår psyke, eller via intense kryssforhør av naturen selv, får glimt av den reelle virkelighet mister vi "munn og mæle". Det forteller to ting:
1. Det er en vesensforskjell mellom språk og reell virkelighet. Og ofte har begrepene en tendens til å oppleves som virkelighet i seg selv. Men glimt av virkeligheten antyder at de bare er fornuftens produkter. Nå diskuterer de lærde heftig om matematikken er en iboende egenskap ved naturen, det er en oppfatning som stammer fra Pytagoras. I dag er det imidlertid kritiske røster som hevder at disse egenskaper er tillagt naturen av oss mennesker, og oppstår som en del av et komplisert et samspill mellom iakttager (menneske) og det iakttagende (naturen).
2. Språket har klare grenser når det gjelder å beskrive virkeligheten som den er. Det er et kommunikasjonsmiddel med begrensninger som avhenger av begrepene.
Så til det spørsmålet som har beskjeftiget Østens filosofer i århundrer: Hvordan kan vi mest mulig klare å tilnærme språket til virkeligheten?
I vesten fikk vi idealet fra den greske filosofi. Euklid konstruerte sin geometri ved bruk av et aksiomatisk deduktivt system med klare veldefinerte begreper. F.eks.: "En linje er en lengde uten bredde" Dette har etterhvert blitt vestens ideal. Alle moderne vitenskaper har mer eller mindre prøvd å etterstrebe dette idealet. Men nå viser fysikken oss at dette idealet har klare grenser. De vitenskapelige modeller er bare tilnærmelser til virkeligheten; de er kart over virkeligheten. At de aldri kan bli i stand til å beskrive virkeligheten helt og fullstendig uttrykkes slik av Einstein:
"I det omfang matematikkens lover gjelder for virkeligheten, er de ikke sikre, og i det omfang de er sikre, gjelder de ikke for virkeligheten"[6]
Fritjof Capra hevder i sin bok "Fysikkens Tao" at unøyaktighet i språket er en nødvendighet for å oppnå størst mulig tilnærming mellom språk og virkelighet:
"Den vitenskapelige abstraksjonsform er meget virkningsfull og hensiktsmessig, men vi må betale en pris for den. Etterhvert som vi har definert vårt begrepssystem med større nøyaktighet - gjør det mere strømlinjet og oppstiller strengere regler for de innbyrdes forbindelser- fjerner det seg stadig mer fra den virkelige verden- Tenker vi igjen på Korzybskis sammenligning mellom kartet og landskapet, kan vi si, at det alminnelige språk er et kart, som på grunn av sin iboende unøyaktighet har en viss bøyelighet, således at det i noen grad kan smyge seg etter landskapets krumme former. Når vi gjør kartet mere stivt, forsvinner denne bøyeligheten etterhvert, og med det matematiske språk har vi nådd et punkt, hvor forbindelsene til virkeligheten er så svake at forholdet mellom symbolene og vår sansemessige erfaring ikke lengre er åpenbar. Derfor er vi nødt til å supplere våre matematiske modeller og teorier med språklige fortolkninger, hvorved vi igjen anvender begreper, som kan forstås intuitivt, men som er en smule tvetydige og unøyaktige"
Det vi aner her er et grunnleggende problem, som gjelder for alle abstrakte språk. Vi kan tenke oss dette problem som en konflikt mellom sikkerhet mot informasjons-forvrenging og språkets anvendelighet til å beskrive. Denne konflikten er på det nærmeste et paradoks som viser at språket aldri kan bli et ideelt kommunikasjons-middel. Paradokset kan utrykkes slik: Jo klarere vi taler, jo mindre sier vi. Innenfor de forskjellige filosofiske skoler finner vi forskjellig vekt på visse sider av dette paradokset. Vi har allerede nevnt vestens Euklidske ideal, som søker å minimalisere begrepsforvrengingen. På den annen side har vi den orientalske filosofi, som har gått til den motsatte ytterlighet, nemlig å tale i gåter og i paradokser, eller å si ingenting. Her er noen eksempler:
En munk spurte Fuesko Ensho: "Hvis både tale og taushet er utillatelig, hvordan kan man da bestå uten å gjøre feil?" Mesteren svarte:
«Jeg husker alltid Kiangsu i mars åkerhønenes skrik og de mange duftende blomster»
Da zen-mesteren Daito møtte keiser Godaigo, som studerte zen-buddhismen, sa han:
«Vi skiltes for mange tusen 'kalpaer' siden. Men vi har allikevel aldri vært adskilt et øyeblikk. Vi sitter ansikt til ansikt dagen lang, men vi har aldri møtt hverandre.»
En munk bad om veiledning og sa til Bodhidharma: «Jeg har ingen sinnsro. Vær vennlig å berolige mitt sinn»
«Kom hit med sinnet ditt» svarte Bodhidharme «Så skal jeg berolige det»
«Men når jeg leter etter mitt sinn», svarte munken, «kan jeg ikke finne det?»
«vær så god», sa Bodhidharma, «så har jeg beroliget det».
En munk sa til Joshu: «Jeg er kommet helt til klostret. Vær god å gi meg veiledning».
Joshu spurte: «Har du spist risgrøten din?»
- «Jeg har spist den.»
- «Da kan du gå å vaske bollen din»
En munk oppsøkte en gang Joshu og spurte han:
«Har en hund buddhanatur, eller har den ikke?»
«Mu» svarte zen-mesteren.
(Mu betyr noe slikt som nei, eller ikke, men det er også et uttrykk for den levende, dynamisk virkende buddhanatur)
Her er noen «Mu-kaan'er»:
Hva var ditt opprinnelige ansikt - som du hadde før dine foreldre unnfanget deg?
Du kjenner lyden av to hender som klapper. Hva er lyden av en hånd som klapper?[7]
Denne siste kan nok virke forvirrende på oss voksne, men jeg prøvde den på min 6-årige datter Monica, og for henne var den ikke noe problem: «Slik», sa hun, og klappet seg på kinnet.
Fra gresk filosofi kjenner vi til lignende retninger, særlig hos Heraklit finner vi mange paradoksale uttalelser f.eks. «Vi er og vi er ikke», og «vi både stiger og stiger ikke ned i samme elv» [8]
Begge uttalelser er klart i strid med kontradiksjons-prinsippet, men de har klare berettigelser. Praktisk sett er en elv aldri den samme. Idet vi stiger ned i elven renner vannet forbi og elven forandrer seg; den er ikke den samme. Heraklit, lærte at «alt forandrer seg». Det er en klar parallell til orientalsk tenkning hvor forandring regnes for å være et grunnleggende trekk med naturen. I et slikt system skjer forandringene gjennom motsetninger. Vi har de kinesiske begrepene yin og yang som er et uttrykk for disse motsetningene. Vi har begrepet «tao» som betyr vei. Det er forandringenes vei, den stadige pendlingen mellom yin og yang. Den såkalte dialektikken som har røtter like tilbake til Heraklit, men som finnes i moderne form hos Hegel og Marx, er en klar parallell til denne type tenkning. Den er på ingen måte forenelig med tradisjonell logikk. Dialektikken er læren om syntese gjennom motsetninger, og de uendelige forandringer som oppstår gjennom den. Motsetningene har fått navnene "Tese" og "anti-tese" som gir en syntese. Denne syntesen kan igjen være en tese som får sin antitese, og en ny syntese oppstår. Se figuren under [9]
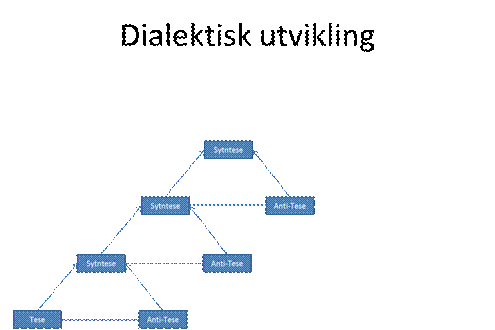
Det er ikke vanskelig å finne eksempler hvor denne modellen er meget anvendelig. Vi har allerede sett den i aksjon i modellen for konstruktiv diskusjon, hvor vi oppnår en økning av kunnskap gjennom motsetninger. Modellen dukker også opp i flere andre sammenhenger senere. Det vi ser her er at vanlig tradisjonell logikk på ingen måte er dekkende for alle områder av virkeligheten. Det har ledet mange såkalte mystikere til en generell mistillit til fornuften. Dette uttrykkes best ved å ty til paradokser. Paradokser er som regel forårsaket av språket selv. Våre glimt av virkeligheten bak, antyder imidlertid at hinsides språket utslettes paradoksene fordi språket ikke lengre skaper dem.
Det religiøse språk beskjeftiger seg ofte med de ting som ligger utenfor vårt domene, derfor er det religiøse språk spekket av symboler, paralleller og paradokser. Det samme gjelder den kunstneriske litteratur. Der er en hel vitenskap utviklet for tolkning av dikt, poesi og romaner. Personlig må jeg innrømme at jeg tviler på riktigheten av en slik forskning. Og med riktigheten, mener jeg, at der skulle finnes universale metoder som klargjør det budskapet forfatteren forsøker å meddele. Dette begrunner jeg på to måter:
1. Når forfatteren må ty til symbolikk, paralleller og paradokser for å kunne meddele seg, antyder det i seg selv, at det han prøver å si er uutsigelig; det må forstås intuitivt gjennom en levendegjøring av begrepene. Av den grunn unndrar poesien seg vitenskapelige metoder, fordi de forsøker å si, i klartekst det som ikke er mulig å si.
2. På grunn av tvetydigheten som må ligge i begrepene lar teksten seg forme av leseren; leseren legger sin oppfatning i begrepene, og får dermed sin egen mening ut av det.
Dette gjelder for øvrig ikke bare poesi, det gjelder all tolkning av kunst i det hele. Straks kunsten blir gjenstand for fortolkninger mister den en del av den fortryllelse som gjør kunst til kunst. Enklest ser vi kanskje dette når det gjelder vitser. Hvis du ikke forstår en vits umiddelbart, blir den tåpelig når noen prøver å forklare den for deg. Straks man begynner å forklare hva som er morsomt med en vits, blir det hele krampaktig, og på mange måter dødsens alvorlig. Vitsen dør. Det er fornuften som dreper den. Slik er det også med kunsten. Verbale fortolkninger av musikk, virker tragikomisk på meg. Musikken må leve, dens rytmer må oppleves, før man får noe ut av den. Men musikken har, som all annen kunst, forskjellig virkning på individene. Den oppleves forskjellig. Den lever et sitt eget liv hos lytteren, et liv som kanskje er fjernt fra den opplevelse den gav komponisten. Det er dette som gjør kunsten så spennende, så uforutsigbar, så uutsigelig. Slik er det også med det religiøse språk. Begrepene blir levende, og lever sitt eget liv hos hver enkelt av oss. dersom begrepene ikke lever, blir religionen død for oss; dens utsagn blir banale og uforståelige.
Vi har sett litt på tolkning av enkle utsagn. Vi har sett at tolkningen avhenger av logisk form og begrepenes innhold. Den logiske formen i et utsagn er nokså statisk, det er gjennom begrepenes dynamikk at uklarheten oppstår. Denne uklarheten, hevdes det, kan stort sett elimineres gjennom å studere den kontekst utsagnet inngår i. Dette, tror jeg, er en sannhet med mange og store modifikasjoner. På bakgrunn av betraktningene ovenfor vil jeg innføre begrepet elastisitet, i forbindelse med tekst. Det er grader av elastisitet. Graden er gitt av den type tekst som foreligger. Det rene matematiske språk, og programmeringsspråkene er stive språk; de har ingen elastisitet, det er ikke mulig å omtolke budskapet i dem. De har entydig informasjon, som kan utledes ved de metoder som gjelder for det språket. Dernest har vi det vitenskapelige språket; fagspråkene innenfor de forskjellige disipliner. Fagspråkene består av sett med begreper som inngår i en faglig referanse-ramme. [10] Dette gjør at den felles oppfatningen av begrepenes innhold og deres sammenheng med hverandre er nokså ens innenfor disiplinen. Formbarheten av slike tekster er derfor liten. Så har vi de naturlige språkene. Her er det slutt på de entydige definisjonene. I de naturlige språkene finnes de samme begreper innenfor mange forskjellige sammenhenger, og får forskjellig betydning alt etter hvordan de brukes. Her er vi klart avhengig av konteksten for å kunne nærme oss det innhold forfatteren har lagt i teksten. Så lenge forfatteren lever har vi jo fasiten tilgjengelig. Men de fleste forfattere dør jo etter hvert og da oppstår problemene. Man begynner å diskutere, hva mente forfatteren egentlig med det og det? Det oppstår hypoteser og forskjellige tolkningsalternativer. Selv filosofer, som jo er kjent for å være nokså klare i sin anvendelse av begreper, blir gjenstand for diskusjon. Det har vært hevdet at selv Kants skrifter skal være fulle av selvmotsigelser. Mange av dem eksisterer nok fordi bruken av begrepene ikke er konsekvent gjennom hele verket. Det er umulig å få til, så lenge vi anvender det naturlige språk.
Det naturlige språk danner grunnlaget for den kunstneriske og religiøse språkbruk. Men begrepene har svært ofte uvanlige og uklare innhold. I disse tekstene er elastisiteten svært stor. Språket blir levendegjort i den enkeltes bevissthet i den grad han suggereres inn i teksten. Her kan man stille spørsmålet om det virkelig er mulig å gi begrepene innhold bare ved å endre konteksten. Det avhenger selvfølgelig fra tekst til tekst, men elastisiteten er så stor at selve konteksten er formbar i seg selv.
Når vi mennesker oppfatter ting og lærer ting skjer det med utgangspunkt i et såkalt psykologisk skjema[11]. Det tilsvarer nøkkel eller protokoll i min mer data-orienterte ip-teori. Vår arv og den påvirkning vi eksponeres for som barn danner grunnlaget for utviklingen dette skjema. Vi lærer lett de ting som enkelt lar seg føye inn i dette skjema, mens ting som krever en endring av selve skjemaet blir nesten umulig å lære. Et psykologisk skjema er den måten vi etterhvert kommer til å betrakte verden, som en helhet, på. Det er den enkeltes personlige refeansremodell. Religiøst og kunstnerisk språk må ha en viss evne til å tilpasse seg et slikt skjema for å kunne gi resonans i bevisstheten. Man snakker om å "være på bølge-lengde" med noen, eller om å "samstemme". Nå er det klart at et slikt skjema ikke nødvendigvis stivner like etter puberteten, det er individuelt, men ettersom alderen stiger øker stivheten. dette kommer sannsynligvis av den konvergente fornufts økende dominans, i det psykologiske system, etter hvert som alderen øker.
Så spørs det hvem som formes mest, er det teksten eller er det, skjema? Jeg har grunn til å tro at helheten i en slik tekst kan omformes til det ugjenkjennelige. En slik mulighet til modellering av tekst bygger på fire grunnpilarer:
1. Bruk av overordnede tankesystemer (referanse-modeller)
3. Konstruksjon av underforståtte sammenhenger
4. Inkonsekvent tolkningsmetode
Vi skal huske at den logiske struktur er mest fastlåst på setningsnivå, ikke på kontekst-nivå. Når vi snakker om logisk struktur på kontekst-nivå er det spørsmål om konsistens i teksten. Danner tolkningene selv-motsigelser? Er begrepene konsekvent anvendt? Ingen av spørsmålene er egentlig 100 % berettiget, for hvem har vel garanti for at forfatteren virkelig ikke motsa seg selv? Og hvem kan garantere at ikke forfatteren har brukt begrepene på en inkonsekvent måte? Dette er krav som ikke nødvendigvis er oppfylt i teksten i utgangspunktet. Men enhver tolkning av en tekst som antyder dette mister egentlig troverdighet. Hvis vi ikke går ut fra at teksten ikke er feilfri i utgangspunktet, hvordan skal vi vite hvilke feil som er gjort?
I nesten enhver tekst av dette slaget kan selvmotsigelser innføres eller fjernes ved hjelp av begrepsforklaring. Det er klart derfor ingen klarer å finne selvmotsigelser i Bibelen eller Koreanen, som overbeviser den troende.
Konklusjonen er egentlig den samme som før antydet: I forsøket på å beskrive den opplevde virkelighet tyr forfatteren til meget formbart språk. Det går på bekostning av informasjons-påliteligheten. Over tid, og med kultur og språk får vi enorme problemer med informasjonsforvrengingen. Men det levende språket gjør sin virkning likevel, fordi det er formbart. Det oppfattes og forstås subjektivt, og de lærde kommer i strid med hverandre.
Hva kan vi gjøre med dette? Skal vi slutte å tolke tekster, etter at forfatteren er død? Nei, det ville være den absolutte resignasjon. Det ligger en mengde informasjon i de gamle tekster, men vi kan aldri feste lit til andres, eller egne, tolkning av dem. Ved vår vurdering av tolkningshypoteser kan følgende nøkkelspørsmål være nyttige:
1 Hvor godt passer hypotesen med de data som nevnes? Er f.eks. de opplysninger og teorier man gjør bruk av når man utleder konsekvensene av hypotesen rimelige, eller virker de ad hoc dvs. virker teorien "episykler" som bare er innført for å redde hypotesen, eller kan de underbygges med argumenter og belegg?
2 Hvor godt passer hypotesen inn med de data som ikke nevnes, f.eks. andre avsnitt i teksten?
3 Selv om hypotesen passer inn med alle data bør vi også spørre: finnes det andre hypoteser eller teorier som passer minst like godt inn med alle data og som er enklere? [12]
Disse spørsmålene er ikke nødvendigvis anvendbare kun i forhold til tekst-tolkning, men også i tolkning av alle slags data.
Når vi søker å tolke en tekst er det viktig at vi har klart for oss hvilket formål vi har med tolkningen. Hva er det vi ønsker å finne ut? Formålet med tolkningen kan være helt avgjørende for resultatet. En vanlig feil her er at man blander sammen forskjellige tolknings-formål. Et viktig skille her er skille mellom intensjon og konvensjon. Jeg vet av egen erfaring at mine tekster ikke alltid uttrykker det jeg ønsker å si. Ut fra det kan jeg konkludere at forfatterens intensjon med sitt verk kan frikobles fra hva verket faktisk sier. Ønsker vi å finne ut hva verket faktisk sier, eller hva forfatteren mente å si? Tolker vi kunstnerisk litteratur er faktisk det siste alternativet det mest nærliggende. Grunnen til dette er tidligere belyst. Tekster av denne art oppfattes forskjellig alt etter hvem som ser. Det er det som gjør kunsten spennende. Når vi søker å tolke et verk på denne måten er det likevel flere tin g å ta stilling til. I henhold til hvilken konvensjon skal verket tolkes. Den vanlige løsningen her er å forsøke å tolke verket slik en tiltenkt mottaker-gruppe ville ha tolket det. Derfor heter det ofte at man trenger selve verket pluss kjennskap til dets mottaker-gruppe for å kunne gi en "riktig" tolkning av verket. Det vi her skal merke oss er at mottakergruppen også var en del av forfatterens intensjoner. Etter min mening bør man ikke henge seg opp i alt for strenge regler her. Det finnes, etter min mening, ikke noe fasitsvar på slike tolkninger. Et like interessant spørsmål kan jo være: hva sier verket meg, og hvorfor? eller: hvordan ser det ut til at den og den har forstått verket?
Dersom vi velger forfatterens intensjon med verket som mål for vår tolkning, blir spørsmålet et annet: hva var det forfatteren egentlig prøvde å si? Dersom vi skal kunne finne ut av det må vi ha en anelse om hva forfatteren la i de begreper han anvendte. Her finnes det selvfølgelig grenser for hvor langt forfatteren kan gå i ukonvensjonell anvendelse av begreper. Men også i denne sammenheng er det nyttig å vite hvilken mottakergruppe teksten var tiltenkt. Det kan gi en god pekepinn på hvordan begreper er anvendt og hva slags innhold de har.
En ting er viktig å få med seg her: det er kun gjennom denne siste metoden at ekte kommunikasjon kan foregå. Derfor har også jeg lagt størst vekt på denne siden av teksttolknings-problematikken.
Det finnes grader av modellerbarhet i alt abstrakt språk. Jo mindre elastisk, desto fjernere er vi fra virkeligheten. Jo større elastisitet, desto mindre informasjonspålitelighet. Matematikken, representerer den ene ytterlighet, med klare veldefinerte begreper, og full informasjonspålitelighet. Kunst-språk og religiøst språk representerer den andre ytterlighet, der er begrepene levende og subjektivt, intuitivt oppfattet. Denne type språk formes sannsynligvis mer av individet enn individet formes av teksten. De er derfor uegnet til sikker informasjonsoverføring.
Se her
Se her
Se her
Se her
[1] Dette er eksempel på en definisjon og ikke nødvendigvis noe allmenngyldig. Dette var før begrepet ekteskap ble et stridstema i forhold til homofile.
[1]. Definisjonene er hentet fra Kari Opdal's bok "Logikk" side 29
[2]. eksempler på det er gitt i Kari Opdal's bok, hvor også det siste eksemplet var hentet fra.
[3].Hentet fra en artikkel i "Evangeliets sendebud" Nr 10, 1989 side 26.
[4].Fritjof Capra "Fysikkens Tao" side 47
[5].Fritijof Capra "Fysikkens Tao" side 35
[6]. Fritijof Capra "Fysikkens Tao" side 43
[7].Alle disse sitatene er hentet fra forskjellige steder i "Fysikkens Tao"
[8]. Sitatene er hentet fra Kari Opdahl's bok "Logikk"
[9]. Figuren er hentet fra Kari Opdahl's bok "logikk"
[10]. Se 2.2.1 om referanse-modell
[11]. Begrepet skjema ble innført av Piaget, som et uttrykk for de kognitive strukturer som inneholder den erfaring og viten som individet på et gitt tidspunkt har.
Barne og Ungdoms-psykologi side 53
[12]. "Argumentasjons-teori, vitenskapsfilosofi og språk" side 96